LeetCode 算法题

• 简单
  • 两数之和
  • 回文数
  • 罗马数字转整数
  • 合并两个有序链表

每天一道，没坚持下去

简单

两数之和

题目地址 (opens new window)

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9

输出：[0,1]

解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6

输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6

输出：[0,1]

• 解题思路:

• 方法一:

  • 枚举在数组中所有的不同的两个下标的组合
  • 逐个检查它们所对应的数的和是否等于target

• 复杂度分析:

  • 时间复杂度:O(n²),这里n为数组的长度
  • 空间复杂度:O(1),只用到常数个临时变量

class Solution {
    int arr[]=new int[2];
    public int[] twoSum(int[] nums, int target) {
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<nums.length;j++){
            if((nums[i]+nums[j]==target)&&i!=j&&i>j){  
                arr[0]=j;
                arr[1]=i;    
            }
        }
    }
        return arr;    
}
}

• 方法二:查找表法
  • 在遍历的同时，记录一些信息，一省去一层循环，这是“以空间换时间”的想法
  • 需要记录已经遍历过的数值和它所对应的下标，可以借助查找表实现
  • 查找表与两个常用的实现:
    • 哈希表
    • 平衡二叉搜索树
• 复杂度分析：
  • 时间复杂度:O(n),这里n为数组的长度
  • 空间复杂度:O(n),哈希表里最多需要存n-1个键值对

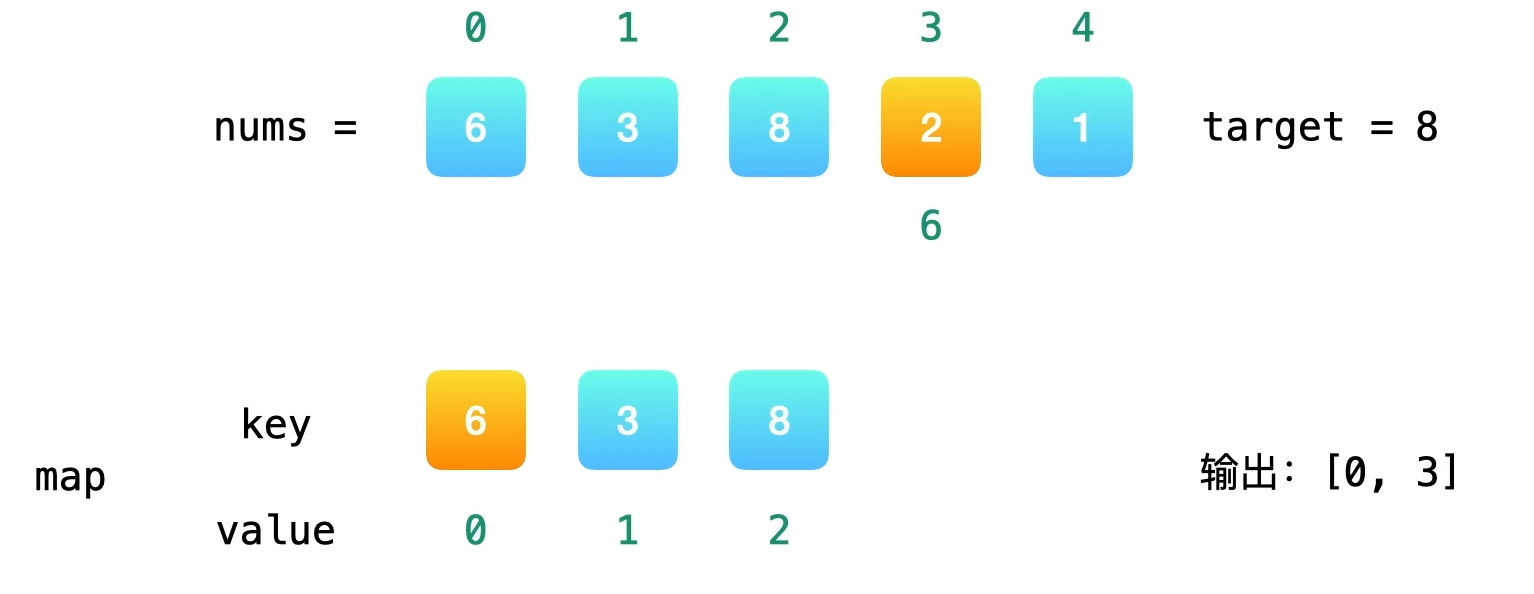
提示

遍历nums,第一个元素6，不在哈希表中，key为6，value为0，存入哈希表；遍历元素3，与之对应的元素应该是target-3=5,5不在哈希表中，key为3，value为1，存入哈希表中;遍历到元素8，与之对应的元素应该是target-8=0,0不在哈希表中，key为8，value为2，存入哈希表中；遍历到元素2，与之对应的元素应该是target-2=6,6在哈希表中；因此6和2就是我们要找的两个元素，对应的下标分别是0,3,将数组[0,3]返回即可，算法到此结束。

class Solution {
    public int[] twoSum(int[] nums, int target) {
 		int len=nums.length;
        Map<Integer,Integer> hashMap=new HashMap<>(len-1);
        hashMap.put(nums[0],0);
        for(int i=1;i<len;i++){
            int another=target-nums[i];
            if(hashMap.containsKey(another)){
                return new int[]{i,hashMap.get(target-nums[i])};
            }
            hashMap.put(nums[i],i);
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}

使用 Map 的containsKey() 方法来检测another是否存在, 如果key存在,则返回i以及与之对应的数的下标hashMap.get(target-nums[i]，如果another不存在则将nums[i]，与之对应的下标i存入哈希表中。

回文数

题目地址 (opens new window)

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。

示例 1：

输入：x = 121

输出：true

示例 2：

输入：x = -121

输出：false

解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数

• 方法一:进阶-反转一半数字
  • 时间复杂度:O(log₁₀(n))
  • 空间复杂度:O(1)

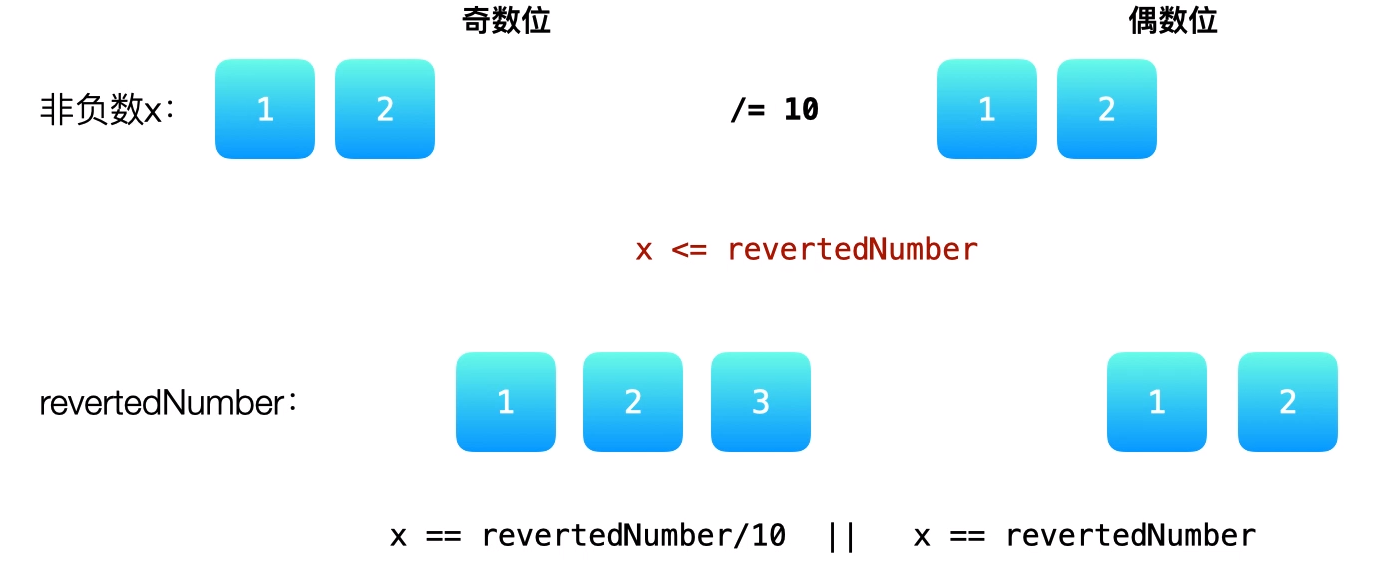
提示

奇数位关于中间数对称，偶数位关于最中间两个数之间对称，x取余10的操作，结果1放在整形变量revertedNumber中，x除以10，舍去最后一位，第一轮迭代；x取余10的操作，整形变量由1变为12，x除以10，第二轮迭代；x越来越小，整形变量越来越大;对于偶数位，迭代终止的条件为x=revertedNumber,对于偶数位迭代终止的条件为x<revertedNumber;奇数位还需一轮迭代，x取余10的操作，整形变量由12变为123，x除以10;对于偶数位，判断数字x和反转后的数字是否相同；对于奇数位，将反转后的数字除以10看是否与x相同

class Solution {
    public boolean isPalindrome(int x) {
        if (x == 0) return true;
        if (x < 0 || x % 10 == 0 && x!=0) return false;
        int reversedNumber = 0;
        while (x > reversedNumber) {
            reversedNumber = reversedNumber * 10 + x % 10;
            x /= 10;
        }
        return x == reversedNumber || x == reversedNumber / 10;
    }
}

• 其他解法

• Java
• Python

class Solution {
    public boolean isPalindrome(int x) {
        StringBuilder sb = new StringBuilder(Integer.toString(x));
        if (sb.toString().equals(sb.reverse().toString())) return true;//reverse()反转字符串
        else return false;
    }
}

class Solution:
    def isPalindrome(self,x:int)->bool:
        s=str(x)
        l=len(s)
        h=l/2
    	return s[:h]==s[-1:-h-1:-1]  #前一半字符串和后一半字符串是否相等

罗马数字转整数

题目地址 (opens new window)

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

• I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

• X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

• C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。

示例 1:

输入: s = "III"
输出: 3

示例 2:

输入: s = "IV"
输出: 4

示例 3:

输入: s = "IX"
输出: 9

示例 4:

输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

题目提示：

• 1 <= s.length <= 15
• s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
• 题目数据保证 s 是一个有效的罗马数字，且表示整数在范围 [1, 3999] 内
• 题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
• IL 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。
• 关于罗马数字的详尽书写规则，可以参考 罗马数字 - Mathematics 。

解题提示

通常情况下，罗马数字中小的数字在大的数字的右边。若输入的字符串满足该情况，那么可以将每个字符视作一个单独的值，累加每个字符对应的数值即可。

例如XXVII可视作X+X+V+I+I=10+10+5+1+1=27。

若存在小的数字在大的数字的左边的情况，根据规则需要减去小的数字。对于这种情况，我们也可以将每个字符视作一个单独的值，若一个数字右侧的数字比它大，则将该数字的符号取反。

例如XIV可视作X-I+V=10-1+5=14。

class Solution {
    Map<Character, Integer> symbolValues = new HashMap<Character, Integer>() {{
        put('I', 1);
        put('V', 5);
        put('X', 10);
        put('L', 50);
        put('C', 100);
        put('D', 500);
        put('M', 1000);
    }};
    public int romanToInt(String s) {
        int ans = 0;
        int n = s.length();
        for (int i = 0; i < n; ++i) {
            int value = symbolValues.get(s.charAt(i));
            if (i < n - 1 && value < symbolValues.get(s.charAt(i + 1))) {
                ans -= value;
            } else {
                ans += value;
            }
        }
        return ans;
    }
}

• 复杂度分析
  • 时间复杂度：O(n)，
  • 空间复杂度：O(1)。
• 其他解法

class Solution {
    public int romanToInt(String s) {
        s = s.replace("IV","a");
        s = s.replace("IX","b");
        s = s.replace("XL","c");
        s = s.replace("XC","d");
        s = s.replace("CD","e");
        s = s.replace("CM","f");
        int res = 0;
        for (int i = 0; i < s.length(); i++) {
            res += getValue(s.charAt(i));
        }
        return res;
    }
    private int getValue(char ch){
        switch(ch){
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            case 'a': return 4;
            case 'b': return 9;
            case 'c': return 40;
            case 'd': return 90;
            case 'e': return 400;
            case 'f': return 900;
       }
       return 0;
   } 
 }

合并两个有序链表

题目地址 (opens new window)

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

public class ListNode {
    int val;
    ListNode next;
    ListNode() {}
    ListNode(int val) { this.val = val; }
    ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列

方法一：递归

思路

我们可以如下递归地定义两个链表里的 merge 操作（忽略边界情况，比如空链表等）：

也就是说，两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。

算法

我们直接将以上递归过程建模，同时需要考虑边界情况。

如果 l1 或者 l2 一开始就是空链表 ，那么没有任何操作需要合并，所以我们只需要返回非空链表。否则，我们要判断 l1 和 l2 哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空，递归结束。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        } else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

复杂度分析

• 时间复杂度：O(n+m) ，其中 n 和 m 分别为两个链表的长度。因为每次调用递归都会去掉 l1 或者 l2 的头节点（直到至少有一个链表为空），函数 mergeTwoList 至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即 O(n+m)。

• 空间复杂度：O(n+m)，其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m次，因此空间复杂度为 O(n+m)。

方法二：迭代

思路

我们可以用迭代的方法来实现上述算法。当 l1 和 l2 都不是空链表时，判断 l1 和 l2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

算法

首先，我们设定一个哨兵节点 prehead ，这可以在最后让我们比较容易地返回合并后的链表。我们维护一个 prev 指针，我们需要做的是调整它的 next 指针。然后，我们重复以下过程，直到 l1 或者 l2 指向了 null ：如果 l1 当前节点的值小于等于 l2 ，我们就把 l1 当前的节点接在 prev 节点的后面同时将 l1 指针往后移一位。否则，我们对l2 做同样的操作。不管我们将哪一个元素接在了后面，我们都需要把 prev 向后移一位。

在循环终止的时候， l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表是非空的，它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。

下图展示了 1->4->5 和 1->2->3->6 两个链表迭代合并的过程：

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode node = new ListNode(0);
        ListNode current = node;
        while (list1!=null && list2 != null) {
            if(list1.val < list2.val) {
                current.next = list1;
                current = current.next;
                list1 = list1.next;
            } else {
                current.next = list2;
                current = current.next;
                list2 = list2.next;
            }
        }
        if(list1 == null) {
            current.next = list2;
        } else {
            current.next = list1;
        }
        return node.next;
    }
}

复杂度分析

• 时间复杂度：O(n+m)，其中 n 和 m 分别为两个链表的长度。因为每次循环迭代中，l1 和 l2 只有一个元素会被放进合并链表中， 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。

• 空间复杂度：O(1)。我们只需要常数的空间存放若干变量。